Кратка Теория за Несиметричната (Свободна) Рамка
Основни Принципи и Дефиниция
Наименованието на полезния модел, съгласно Патентното Свидетелство за Промишлен дизайн, издадено на 21.04.2003 г., е "несиметрична декоративна рамка". Този патент включва 10 типови проекта на всички видове свободни рамки, съгласно изложената по-долу кратка теория.
Името идва от формата на рамката, чийто контур образува несиметрична равнинна фигура. Ако геометричният център на тази фигура се приеме за начало на координатната система, то фигурата няма симетрични части спрямо никоя от осите си.
Основният принцип на несиметричната декоративна рамка е: Да има пълна свобода при избора на нейната форма. Тази произволна форма не трябва по никакъв начин да наподобява тялото на човек, животно, растение или части от тях; всяко съвпадение би било съвсем случайно.
Трите Основни Вида Рамки
Несиметричната декоративна рамка най-общо може да се раздели на три основни вида:
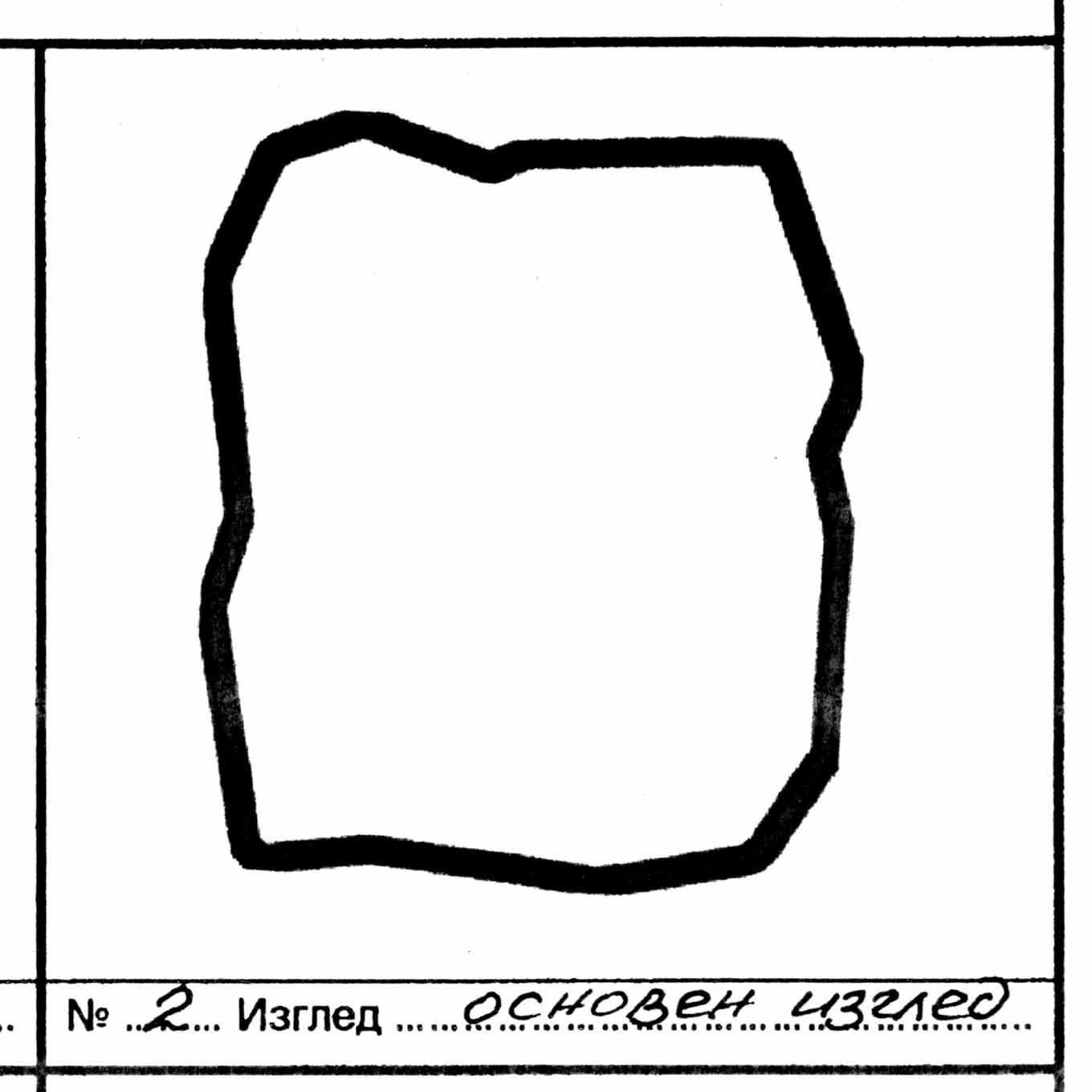
I. Крива Несиметрична Декоративна Рамка: Контурът ѝ представлява произволно крива, затворена линия.
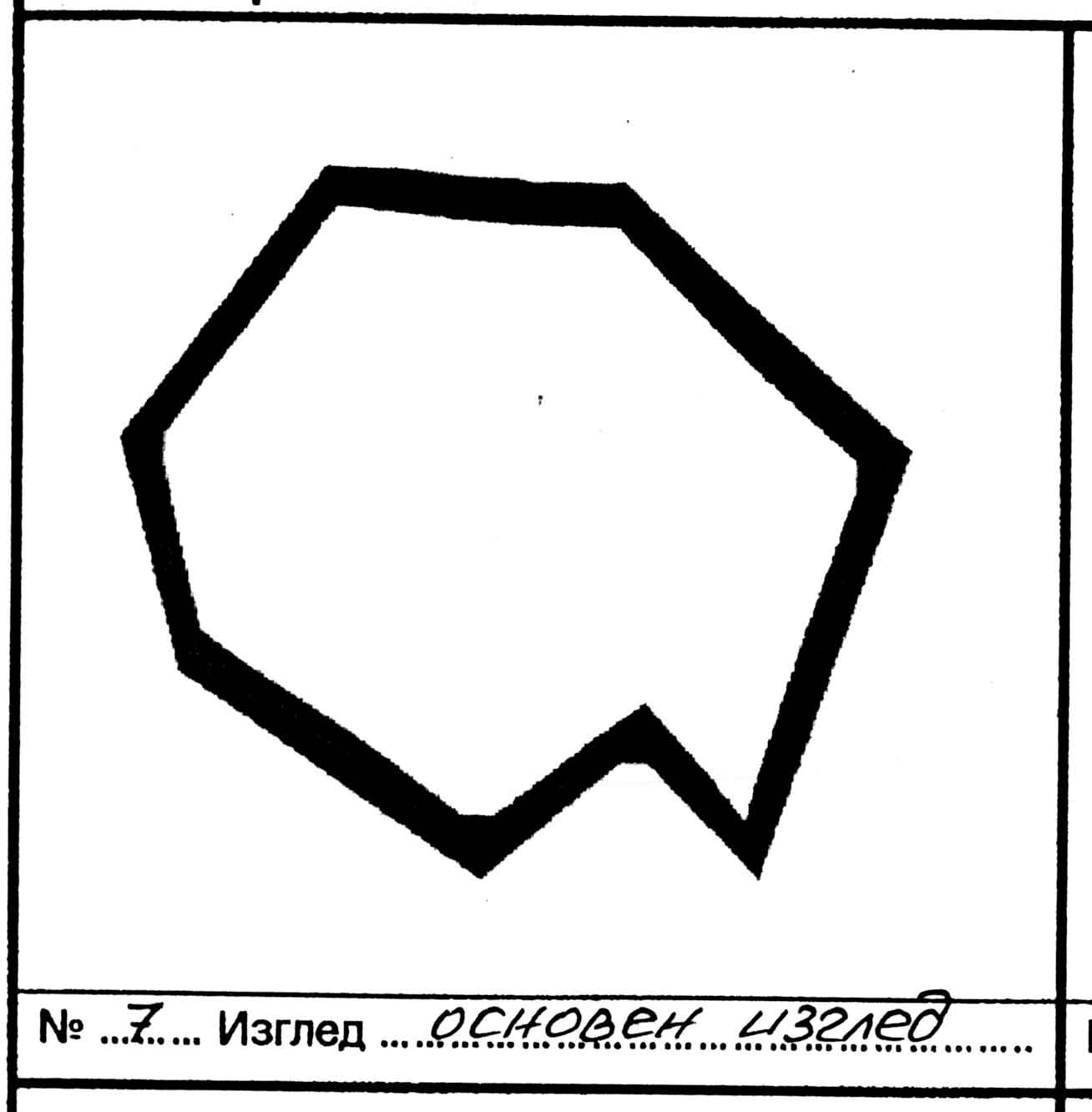
II. Ъглова Несиметрична Декоративна Рамка: Контурът ѝ представлява многостенен неправилен многоъгълник.
III. Комбинирана Несиметрична Декоративна Рамка: Контурът ѝ представлява комбинация от първите два вида, т.е., една част от него е с крива форма, а останалата е ъглова.
При тези 3 основни вида има пълно съвпадение на външната и вътрешна свободни линии, които оформят самата рамка.
Подвидове Несиметрични Рамки
Освен трите основни вида, съществуват и няколко подвида:
| Подвид | Външен Контур | Вътрешен Контур | Описание / Ключова Разлика |
|---|---|---|---|
| А/ | Крива затворена линия | Крива затворена линия | Двете линии не са идентични. |
| Б/ | Начупена (ъглова) затворена линия | Начупена (ъглова) затворена линия | Двете линии не са идентични. |
| В/ | Симетричен (правоъгълник, квадрат, елипса, кръг, трапец, конус, ромб или правилен многоъгълник) | Свободна крива затворена линия | Външният контур е симетричен, а вътрешният е свободна крива. |
| Г/ | Симетричен (правоъгълник, квадрат, елипса, кръг, трапец, конус или правилен многоъгълник) | Крива начупена ъглова затворена линия | Вътрешният контур е асиметрична ъглова линия, а външният е симетричен. |
| Д/ | Асиметрична крива затворена линия | Симетричен (правоъгълник, квадрат, елипса, кръг, трапец, конус, ромб или правилен многоъгълник) | Външният контур е асиметричен, а вътрешният е симетрична фигура. |
| Е/ | Асиметрична ъглова затворена линия | Симетричен (квадрат, правоъгълник, елипса, кръг, трапец, конус или правилен многоъгълник) | Външният контур е асиметричен ъглов, а вътрешният е симетричен. |
Приложение и Технология на Изработка
Областите, където асиметричната рамка може да намери приложение, са: Изобразителното изкуство, Художествената фотография и Дизайн на предмети за дома.
Примери от Галерията с Модели
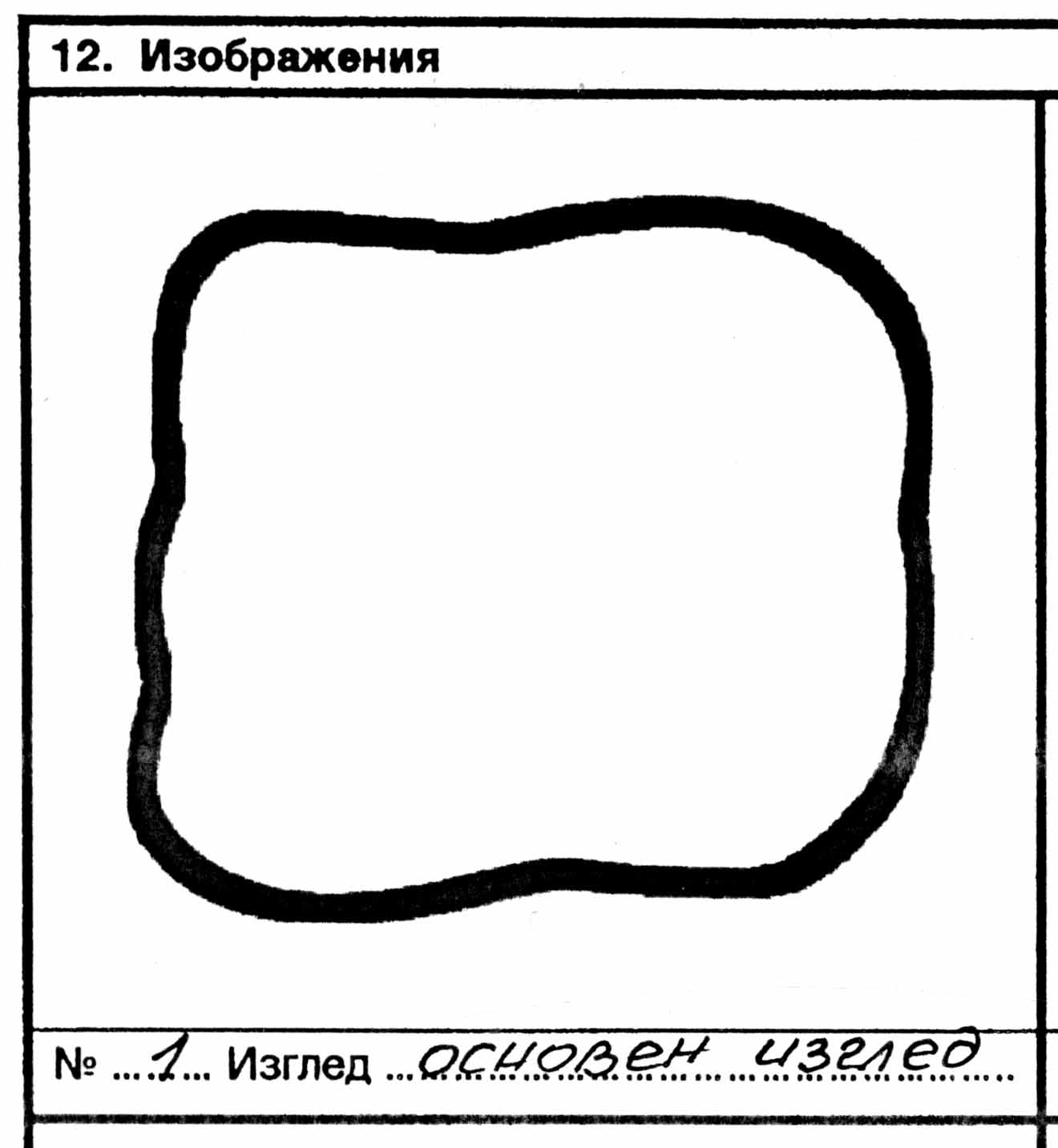
Модел тип 1 - Крива рамка

Модел тип 2 - Ъглова рамка
Модел тип 6 - Комбинирана рамка

Модел тип 7 - Асиметрична форма

Модел тип 8 - Свободна крива
Модел тип 10 - Динамична форма
I. Крива Свободна Рамка (Цяла или Съставна)
- Цялата рамка може да се изработи от естествен материал, изкуствени материали или метални профили.
- Рамката може да бъде с уникална форма, без да се повтаря или шаблонизира.
- Съвременни методи като 3D принтирането и лазерното моделиране могат да се приложат.
- Съставната рамка може да се изработи от отделни дървени сегменти от висококачествена дървесина, които се сглобяват и декорират.
II. Ъглова Свободна Рамка (Само Съставна)
- Ъгловата несиметрична рамка (неправилен многоъгълник) може да бъде само съставна.
- Тя може да се изработи от съществуващите на пазара линейни дървени или пластмасови профили.
- При съставните ъглови свободни рамки е от изключителна важност точното спазване на необходимите ъгли.
III. Комбинирана Несиметрична Рамка
- Тя се явява комбинация на криви и ъглови участъци.
- При изработването на същинската рамка се прибягва до начина на изработка на свободната крива рамка.
- Готовите линейни профили са неприложими поради наличието на свободните криви участъци.
- Готови профили могат да се използват единствено при подвидове, които имат строго само ъглови линии (симетрични или асиметрични ъглови контури).